Commençons par remercier l’Observatoire zététique, sur le site duquel nous avons déniché un article reprenant les détails de cette animation. Nous expliquons ici globalement la même chose, à la sauce Dubitariste.

Cet atelier fonctionne très bien avec tous les types de publics : mettez à contribution enfants comme adultes, tout le monde y trouvera son compte.

Il s’agit de prétendre avoir un don de sourcellerie particulier, consistant à détecter de l’eau dans des gobelets. N’en dites pas plus, et demandez à votre public de rester calme pour favoriser votre concentration.

Sur la table, 10 verres sont alignés, dont 5 sont à moitié remplis et 5 sont vides.

Première expérience : vous faites simplement la démonstration de votre don en passant la main par-dessus les verres, transparents et visibles, les yeux ouverts, et vous annoncez (sans vous tromper, à part peut-être volontairement pour le dernier verre) pour chaque verre s’il contient de l’eau ou non. Généralement, le public se moque de vous, et nie votre don sous prétexte que vous aviez les yeux ouverts, ou que vous avez fait une erreur.

Vous pouvez répondre que même si vous aviez les yeux ouverts, vous utilisiez quand même votre don, ou qu’une erreur ne prouve pas que vous n’avez pas de don, car aucun don ne saurait être infaillible. Bref, soyez d’une mauvaise foi outrancière, et profitez-en pour retourner la charge de la preuve : “Je vous sens sceptiques quant à mon don, c’est maintenant à vous de me prouver que je n’ai pas de don !”

A partir de là, toutes les triches possibles vous sont permises pour mettre en échec les expériences de vos participant·es. Mettez au moins à leur disposition des papiers, des stylos et de quoi cacher les verres. Ajoutez si vous le souhaitez du matériel faisant office de fausse piste. Ne leur mettez pas sous le nez, mais faites leur comprendre qu’iels sont libres de créer leur propre expérience. Pour chaque test, les participant·es peuvent prendre un papier et noter vos prédictions ainsi que votre score (le nombre de correspondances entre vos prédictions et la réalité).

Voici quelques triches pour contrer certaines initiatives que j’ai pu souvent observer :

– “Fermez les yeux pendant qu’on mélange les verres, et recommencez le test”. Faites exactement cela : fermez les yeux pendant qu’ils mélangent, puis rouvrez les yeux et recommencez à passer votre main sur les verres. Et oui, le protocole ne précisait pas qu’il fallait garder les yeux fermés !

– “Fermez les yeux pendant qu’on mélange les verres et aussi pendant le test”. Effleurez les verres avec un doigt pour ressentir son poids. C’est très facile avec des gobelets en plastique ou en carton.

– “Fermez les yeux tout du long, et ne touchez pas les verres”. Là, vous êtes mal. Ne vous avouez pas vaincu·e, faites le test, et vous ferez probablement un score moins impressionnant. Justifiez-vous par une hypothèse ad hoc : “En fait, mes paupières fermées arrêtent les ondes aqua-cosmiques qui vont de ma main jusqu’à mes yeux, donc mon don ne fonctionne que si j’ai les yeux ouverts.” Cette étape est intéressante car elle permet de parler du test à blanc : on se met d’accord avec le sourcier sur les conditions de test qu’il juge acceptable. C’est très important, car cela permet aux testeur·euses de se prémunir des hypothèses ad hoc. Une fois que le sourcier a dit que les conditions fixées étaient bonnes, il ne peut plus prétendre que son don ne fonctionne pas dans telle ou telle condition.

– “Pendant que vous fermez les yeux, on couvre les verres avec les boîtes, puis vous rouvrez les yeux et vous recommencez le test.” Là, pas le choix, il vous faut un·e complice qui aura retenu l’emplacement des verres, et vous fera un signe discret quand vous passerez la main au-dessus d’un verre rempli. Si personne ne découvre la triche, prétendez que vous savez lire le langage non verbal, et que vous avez pu deviner l’emplacement des verres grâce aux micro-expressions des participant·es.

– Généralement, il faut que vous mettiez les gens sur la piste du double-aveugle : un groupe de participant·es A mélange les verres et les couvre pendant que vous fermez les yeux. Le groupe de participant·es B ne regarde pas. Puis le groupe A s’en va, le groupe B revient, vous ouvrez les yeux et commencez le test. Le groupe B prend note de vos prédictions, qu’on peut vérifier tous ensemble à la fin en soulevant les boîtes.

Il vous était ainsi impossible de lire le langage non verbal. Cependant, votre complice était toujours dans le coup. Iel demeure parfois insoupçonné·e très longtemps, car iel fait semblant d’aider les participant·es en leur donnant des astuces. Il faut toutefois finir par évoquer l’hypothèse selon laquelle iel triche !

– Enfin, refaites l’expérience sans complice. La plupart du temps, vous ferez un score tournant autour de 5. Les participant·es vous diront alors “Vous n’avez pas de don, maintenant on le sait !”. Si par chance, vous continuez de faire un score au-dessus de 8, il est possible de refaire le test.

Première conclusion

Selon la patience des publics, leur âge, et leur envie d’aller loin dans les explications, voici plusieurs niveaux de conclusion. Le plus important est de ne pas laisser partir les participant·es avec l’idée qu’iels ont prouvé que vous n’aviez pas de don.

5/10 est le score moyen qu’on obtiendrait si on faisait le test plusieurs fois en prédisant au hasard. Imaginez une pièce de monnaie qui ferait les prédictions à votre place : pile = rempli, face = vide. En moyenne elle ferait le même score que vous lors de la dernière étape du protocole.

En vous faisant obtenir des scores semblables à ceux d’une pièce de monnaie, les participant·es n’ont pas prouvé que vous n’avez pas de don, mais que tout se passe comme si vous faisiez vos prédictions au hasard. Peut-être avez-vous réellement un don, mais comme on peut expliquer votre score par le hasard, pourquoi penser que vous avez un don ?

C’est une illustration du principe de parcimonie, selon lequel il est préférable de considérer en priorité les hypothèses explicatives les plus simples. Cela ne veut pas dire qu’elles sont vraies, mais qu’il est coûteux de chercher des explications complexes quand on a une explication simple qui fonctionne très bien. Ici, le hasard suffit à expliquer les scores, alors qu’admettre l’existence du don demanderait d’expliquer son fonctionnement, et bouleverserait des lois physiques.

Deuxième conclusion

Est-ce que faire des scores de 8/10, 9/10 voire 10/10 remettrait en cause l’hypothèse selon laquelle vous prédisez au hasard ?

Un seul très bon score n’est une preuve de rien, car il peut très bien survenir au hasard. D’où l’importance de faire le test plusieurs fois. Mais alors à partir de quand peut-on supposer que le hasard ne suffit plus à expliquer les faits ?

Voici un tableau qui donne les probabilités d’obtenir au moins chaque score, que vous pouvez imprimer et montrer aux participant·es :

Comment le lire : vous avez par exemple 100% de chances d’obtenir au moins 0/10, car n’importe quel score est supérieur ou égal à 0/10. En revanche vous avez 5,5% de chances d’obtenir au moins 8/10 (c’est-à-dire 8/10 ou 9/10 ou 10/10).

Généralement en sciences expérimentales, quand on cherche l’existence d’un phénomène ou quand on teste une efficacité, on fixe le seuil de significativité à 5%. Cela veut dire que si on calcule que le phénomène a moins de 5% de chances de pouvoir s’expliquer convenablement par le hasard, on peut considérer une autre cause jusqu’à preuve du contraire.

Attention, cette “autre cause” n’est pas forcément un don de sourcellerie. On a juste montré que le hasard ne suffisait pas, mais maintenant les recherches des causes possibles restent ouvertes !

Ici, le seuil arbitraire de 5% est presque atteint avec un score de 8/10. Généralement je ne vais pas plus loin dans les explications statistiques, car à ce moment de l’atelier, s’il est fait en grand public, le quota attentionnel des participant·es est quasiment épuisé. Si vous voulez aller plus loin quand le contexte le permet, je donne quelques détails à la fin de l’article.

Ce que je fais plutôt, c’est une illustration du hasard, en demandant aux participant·es de tester leur don. On refait le même protocole : pendant qu’iels sont retourné·es, une personne désignée (qui ne sera pas en contact avec l’animateur·ice) mélange et couvre les verres. Puis l’animateur·ice revient, ainsi que les participant·es. Iels font des prédictions, qu’iels notent sur papier. Enfin on découvre les verres et on note les scores de chacun·e sur un tableau. J’ai l’habitude de dessiner un graphique en direct, qui ressemble de plus en plus à une courbe de Gauss au fur et à mesure que les participant·es viennent se tester. En voilà un exemple issu de notre participation au Village des sciences les 9 et 10 octobre 2021 :

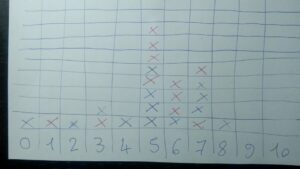
Ce ne sont pas des statistiques précises, mais cela a le mérite d’être très visuel et de “prouver” empiriquement tout ce qu’on vient de dire.

Troisième conclusion

Pour celles et ceux qui en veulent plus, et comprendre ce qu’on peut tirer de cette expérience, voici une sorte de récapitulatif théorique d’un bon protocole expérimental, et des exemples de liens qu’on peut faire avec des situations plus courantes.

J’avais imprimé la liste des points en gras ci-dessous, et j’expliquais à l’oral les explications qui suivent :

1 – Douter de sa position

Ne pas croire ni rejeter par principe. Il faut laisser une place, même petite, au doute.

2 – Chercher si le fait existe avant de vouloir l’expliquer

Si un magicien découpe une personne en deux sur scène, on commence par se demander si la personne a vraiment été coupée en deux, avant de chercher par quel moyen elle survit dans cet état. On cherche des explications théoriques seulement après avoir établi l’existence du phénomène étudié.

3 – Ne pas prendre en compte la bonne ou la mauvaise foi de la personne testée

La sincérité de la personne testée n’a rien à voir avec la réalité des faits prétendus. On teste la prétention et ses effets concrets.

4 – Se mettre d’accord sur ce qu’on teste

C’est le test à blanc évoqué plus haut. Il est impératif de bien définir l’effet attendu et les conditions précises dans lesquelles il se réalise. Sinon, la personne testée peut opérer un déplacement des goals en prétendant qu’un échec était en fait une réussite, ou faire des sauvetages ad hoc en accusant des conditions expérimentales non favorables.

5 – Prendre des mesures claires

Bon, sur cette expérience rien de plus simple, il s’agit de noter si le sourcier dit “eau” ou “pas d’eau”. On peut imaginer que s’il prétendait connaître la quantité d’eau, il aurait fallu se mettre d’accord sur l’unité utilisée, et ne pas se contenter de “pas beaucoup” ou beaucoup”.

6 – Comparer avec un échantillon standard

L’échantillon ici, ce sont les prédictions (et pas les verres en eux-mêmes). Les prédictions testées, ce sont celles du prétendu sourcier, tandis qu’un échantillon standard, ce sont les prédictions des participant·es, qui elleux ne prétendent pas avoir de don. Ainsi on peut observer comment le phénomène se passe en “conditions standard”, et comparer avec les “conditions de test”. Si le phénomène observé est similaire, impossible de conclure à un effet particulier.

7 – Faire un échantillon représentatif

Ce point est peu pertinent dans le cas de notre expérience, car les prédictions ont forcément les mêmes caractéristiques. Mais par exemple, quand on teste l’efficacité d’un médicament, on réalise bien pourquoi il faut éviter de le tester uniquement sur des hommes, ou uniquement sur des personnes de 80 ans : on ne peut alors pas savoir si l’effet du médicament est généralisable à d’autres groupes de la population.

8 – Organiser un double-aveugle

Le prétendu sourcier était “aveugle”, ainsi que les participant·es chargé·es de recueillir ses réponses, car aucun·e ne voyait le mélange des verres. Il est évident qu’il ne faut pas laisser le sourcier voir les réponses… Et concernant les participant·es, cela évitait toute triche de leur part (peut-être motivée à prouver l’absence de don du sourcier), et toute tentative du sourcier de lire du langage non verbal.

9 – Justifier l’inclusion ou le rejet de données

On l’a fait sans l’expliciter : si dans une série de prédictions, le sourcier soulève la dernière boîte pour regarder le contenu du verre, les participant·es vont refuser de noter sa réponse. Dans toute expérience qui collecte des données, il faut justifier pourquoi on prend en note certaines choses et pas d’autres, sinon on peut noter uniquement ce qui va dans le sens de nos a priori, et ignorer ce qui nous dérange. On se prémunit ainsi du cherry-picking.

10 – Considérer l’hypothèse du hasard

Face à un phénomène prétendu (ou n’importe quelle hypothèse), l’expérience mise en place pour le tester n’a pas forcément comme but de remplacer une explication causale par une autre. Il faut envisager la possibilité que le hasard soit la meilleure explication disponible. Certain·es participant·es, même après vous avoir fait effectuer trois fois le test en double-aveugle, et vous avoir vu·e échouer à faire des scores significativement meilleurs que le hasard, continuent de chercher votre méthode de triche (et à part insister sur le fait que le hasard suffit à expliquer ce qui se passe, je ne sais plus quoi leur dire).

Ces points sont des bases utiles pour beaucoup de protocoles visant à tester expérimentalement des hypothèses. Les parallèles avec la médecine sont assez évidents et faciles à comprendre, tant au niveau des enjeux que des sujets, par exemple avec les cas des tests d’efficacité des médicaments, avec de grands échantillons représentatifs, testés en double-aveugle contre placebo.

Si vous faites face à la fameuse question “Mais alors, la sourcellerie ça existe ??”, vous pouvez parler de l’expérience de Munich (je vous laisse vous renseigner ici et là). Cette expérience ne peut pas conclure avec une certitude absolue que la sourcellerie n’existe pas. Cependant, ses résultats indiquent que le hasard suffit à expliquer les prédictions de centaines de prétendus sourciers, dans des conditions expérimentales validées par ceux-ci.

Quelques stats en plus pour la route

Comme promis, quelques détails sur les statistiques, au cas où vous voudriez refaire l’expérience en modifiant des variables. Jetez donc un œil sur le calculateur de probabilités de Geogebra.

Pour l’expérience décrite plus haut, il vous faut d’abord sélectionner “Binomiale”. Le nombre de gobelets est “n”, soit 10. Comme les verres sont soit remplis, soit vides, vous avez une chance sur deux de donner une bonne réponse au hasard, donc “p” = 0,5. Enfin, ce qui nous intéresse ici c’est la probabilité d’obtenir au moins le score k. Sélectionnez donc la borne ” [ “, et tapez le score qui vous intéresse dans “P (k < X)”. Pour k = 8, vous obtiendrez 0,0547, que vous multipliez par 100 pour obtenir une probabilité en pourcentages, soit environ 5,5%.

Ainsi vous pouvez modifier votre expérience à loisir, il vous suffit de connaître la taille de votre échantillon n, et les probabilités p associées à chaque événement. Si vous voulez tester votre capacité à deviner le résultat d’un lancer de dé sur 13 lancers, alors n = 13 et p = 1/6. Dans ce cas, le seuil des 5% est atteint dès lors qu’on arrive à prédire avec succès 5 fois sur 13.

 

Bon, assez discuté, place aux animations ! Faites-nous part de vos expériences si vous avez l’occasion d’animer un atelier similaire 🙂