La pleine lune a-t-elle une influence sur le nombre de naissances ? (spoiler : non)
Commençons par préciser que nous n’avons rien inventé : cet atelier nous a été inspiré par Christophe Michel de la chaîne Hygiène Mentale, que nous remercions pour son aide.
Sur un stand voyant passer beaucoup de public, cet atelier fonctionne très bien car c’est un point d’accroche pour parler d’idées reçues, de méthodes pour les tester, et même de statistiques.
Nous pouvons commencer par demander aux gens s’ils connaissent des idées répandues sur la pleine lune. “On dit que la pleine lune rend plus agité” ; “J’ai entendu dire que les cheveux poussaient plus vite les soirs de pleine lune” ; “Il y a plus de naissances lors de la pleine lune”… Et ce qu’ils en pensent : certaines personnes croient à tout ça, d’autres non, mais ça n’est pas ça l’important. Ces idées sont testables, et on peut trouver une méthode pour évaluer leur vraisemblance.
Comment faire ? Certaines idées sont plus simples à tester que d’autres. Si on cherche à savoir si les cheveux poussent plus vite les soirs de pleine lune, il va falloir recruter des participant·es et mesurer la pousse de leurs cheveux chaque jour sur une longue période. Dans l’absolu faisable, mais long et compliqué. Si on cherche à connaître l’influence de la pleine lune sur l’agitation, il va falloir passer des entretiens, définir ce qu’on entendra comme de “l’agitation”… Faisable, mais très compliqué.
En revanche, évaluer l’influence de la pleine lune sur le nombre de naissances est beaucoup plus simple. Il “suffit” de recueillir les dates de naissances d’un grand nombre de personnes, de retrouver la phase de la Lune correspondante, et de faire quelques calculs avec les données obtenues.
Les participant·es utilisent un éphéméride que nous avons imprimé (merci à Christophe Michel de nous avoir filé le fichier) pour retrouver la phase de la lune correspondant à leur date de naissance (et à celles de leurs ami·es, famille…). Iels peuvent ensuite déposer une bille (ou équivalent) dans un des huit contenants identiques qui leurs sont présentés, chacun correspondant à une phase de la lune, chaque phase contenant le même nombre de jours (et donc le même nombre de naissances si la lune n’a pas d’effet).
En général, au moment où une personne dépose une bille, il est très difficile d’estimer à l’œil nu le nombre de billes correspondant à chaque phase de la lune, et surtout d’en tirer quoi que ce soit. On peut se poser la question ensemble : à partir de quel niveau de bille (ou combien de billes si on veut les compter) est-ce qu’on pourrait conclure qu’il y a davantage de naissances lors de la pleine lune ? Est-ce que 3 billes de plus serait suffisant ? 100 billes de plus ?
C’est là qu’intervient la partie la plus difficile à expliquer : les statistiques. Cependant elle est absolument nécessaire. En effet, les faits ne parlent pas d’eux-mêmes. Dans cette expérience, si la pleine lune n’a pas d’effet sur les naissances, le nombre de billes “pleine lune” a une chance sur deux d’être supérieur à la moyenne. Ainsi, on se sentira légitime de penser “supérieur à la moyenne = influence de la pleine lune validée”. Or c’est plus compliqué que ça.
Nous avions avec nous un ordinateur sur lequel nous inscrivions les résultats dans un tableur, et calculions en direct la p-value associée à la pleine lune, c’est-à-dire la probabilité que le nombre de billes obtenu l’ait été à priori par hasard (dans l’hypothèse où la pleine lune n’a pas d’influence). Pour rendre la p-value plus lisible, nous la multipliions par 100 pour obtenir des probabilités en pourcentage.
Par exemple, si le calcul nous donne 10%, cela signifie qu’on a 10% de chance d’obtenir toutes ces billes “pleine lune” dans une situation où la lune n’a pas d’effet sur les naissances. Cela nous renvoie à la question qu’on se posait un peu plus haut : à partir de quel % estime-t-on que c’est complètement improbable qu’on ait obtenu ce résultat par hasard, et donc qu’on peut penser que la pleine lune a un effet ?
Cette question n’a pas de réponse absolue, écrite quelque part dans la nature, et il faut être clair avec ça. Toutefois, il y a des seuils couramment utilisés en sciences, comme 5% ou 1%. Prenons 5% : cela signifie que pour admettre que nos résultats ne sont pas le fait du hasard, il faut que la probabilité d’avoir obtenu toutes ces billes “pleine lune” dans une situation où la lune n’aurait pas d’effet soit inférieure à 5%. Si c’est le cas, alors ça y est, on peut conclure que la pleine lune a bien une influence sur les naissances ?
Si on ne fait qu’une seule expérience, il se peut que par hasard, on obtienne un résultat significatif. Cela arrivera jusqu’à 5% du temps, car on a décidé que notre seuil était 5%. Aussi, quelconque élément a pu venir fausser nos résultats sans qu’on s’en rende compte. Il faut donc répéter l’expérience plusieurs fois, avec la population la plus grande et diverse possible. Et devinez quoi : l’expérience a déjà été menée maintes fois avant nous, en festival et à l’échelle de la France, et aucun effet significatif de la pleine lune n’a été démontré.
La plupart du temps, vous obtiendrez un graphique plat et une p-value non significative, très supérieure à 5%. Vous pouvez expliquer que cette expérience ne permet pas de conclure une influence de la pleine lune sur le nombre de naissance (et non pas qu’il serait démontré définitivement que la pleine lune n’a aucune influence sur le nombre de naissances).
Si des personnes veulent des réponses, vous pouvez leur assurer que de nombreuses expériences vont dans ce sens également, pour ne pas laisser planer le doute. Mais le plus important selon moi est de passer du temps sur la méthode qui permet d’obtenir ce résultat. L’atelier est participatif et le tableur permet de générer un graphique : les bonnes conditions sont réunies pour parler de statistiques tout en gardant l’attention.
Les visiteurs du Village des sciences (9-10 Octobre 2021) sont-ils davantage nés les jours de pleine lune ?
Nous avons utilisé des haricots rouges secs à placer dans des verres en plastique transparent. Le nombre d’haricots par verre a été compté pendant la première journée puis nous avons essayé de le mettre à jour en direct au fur et à mesure. Il a été recompté à la fin de la deuxième journée.
Ce qui nous intéresse ici est de savoir s’il y a eu plus de naissances les jours de pleines lunes qu’il ne devrait en avoir si la lune n’avait pas d’effet : puisque sur notre éphéméride en moyenne 1 jour sur 8 est un jour de pleine lune (chaque phase lunaire durant 3-4 jours d’affilés), on veut savoir s’il y a plus d’1/8 des visiteurs ayant participé à notre expérience qui sont nés durant une phase de pleine lune. Ainsi nous posons la variable “pleine lune” ayant pour modalités “oui” vs “non”, et l’hypothèse unilatérale “Il y a plus de naissances les jours de pleine lune qu’il ne devrait en avoir par simple hasard”.
Dans ce genre de situation, une simple loi binomiale permet d’établir la probabilité d’obtenir (sans influence de la lune) un nombre précis de résultats positifs (oui, tant de participants sont nés un jour de pleine lune) en connaissant le nombre total de participants (billes/haricots) et la proportion théorique de résultats positifs/participants nés un jour de pleine lune (ici donc 1/8). Sur le logiciel Excel, on peut facilement se servir de la fonction “=LOI.BINOMIALE.N (k;n;p;Cumul)”, où “k” est le nombre de participants nés un jour de pleine lune, “n” est le nombre total de participants, et “p” est la fréquence théorique de participants nés un jour de pleine lune (1/8). Cumul est un outil nous permettant, si on indique “0” d’obtenir la probabilité d’obtenir notre résultat précis, ou si on indique “1” d’obtenir le cumul de la probabilité d’obtenir notre résultat précis et des probabilités d’obtenir un résultat (un nombre de personnes nées lors d’une pleine lune) inférieur.
Puisque ce que l’on souhaite savoir nous est la probabilité d’obtenir (sans effet de la lune) un nombre de naissances égal ou supérieur à celui que nous avons obtenu, la formule adéquate est : “=1-LOI.BINOMIALE.N(k-1;n;p;1)”.
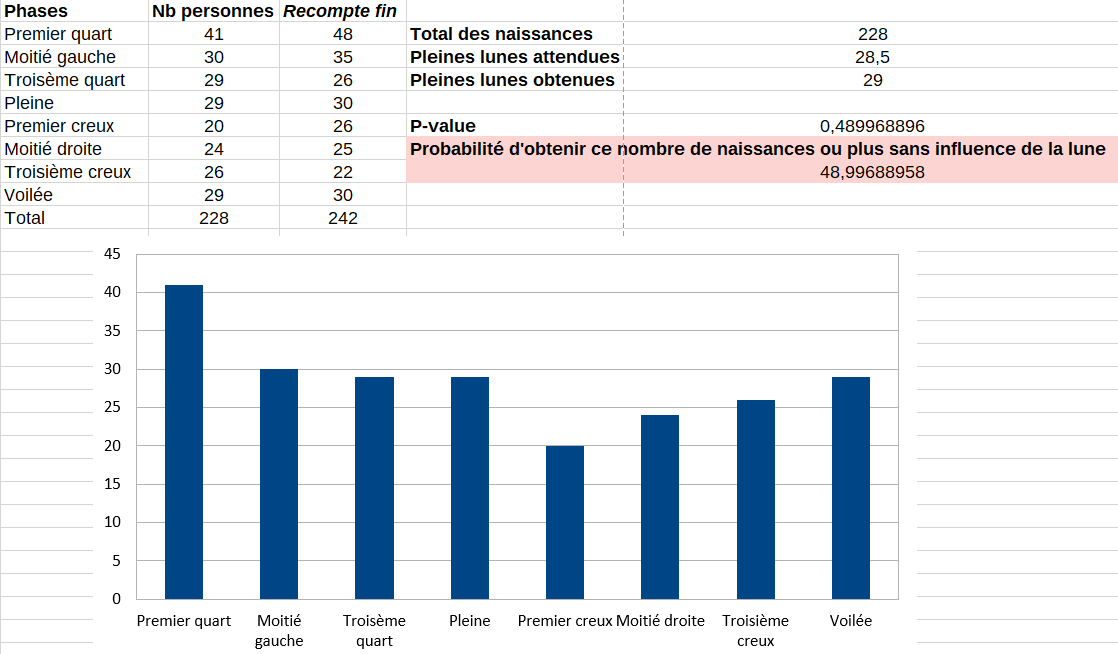
Avec les données récoltées en direct nous avons donc “=1-LOI.BINOMIALE.N(29-1;228;1/8;1)” = 0,49. Avec les données comptées à la fin nous avons donc “=1-LOI.BINOMIALE.N(30-1;242;1/8;1)” = 0,55.
Nous restons donc près d’une chance sur deux d’obtenir autant ou plus de visiteurs étant nés lors de la pleine lune. Nous sommes loin du seuil de 0,05 et n’avons pas de raison de croire à un éventuel effet de la lune sur le nombre des naissances.
On remarquera par contre un étrange résultat (que nous avons testé significatif à 0,05) : il semble parmi les visiteurs en avoir eu plus qui sont nés lors du premier quart de lune ^^ . Ce résultat n’est pas expliqué et ne correspondait pas à l’hypothèse que l’on souhaitait tester ici, mais le hasard fait partie de la vie, et nous pouvons par exemple imaginer que le premier quart de lune (dont le verre était placé le plus à gauche) aurait été confondu (malgré les dessins correspondant entre l’éphéméride et les verres) par certains participants avec le troisième creux.
Néanmoins, un tel résultat dit outlier peut influencer des tests statistiques, et nous pouvons donc relancer les tests en le normalisant(ici en le réduisant) vers la moyenne : “=1-LOI.BINOMIALE.N(29-1;214;1/8;1)” = 0,35 et “=1-LOI.BINOMIALE.N(30-1;222;1/8;1)” = 0,35. Même avec un nombre de naissances dans la moyenne lors du premier quart de lune, la p-value est bien plus élevée que 0,05 et le nombre de naissances de visiteurs lors de la pleine lune reste ainsi près de la moyenne.
Pour les curieux, il aurait fallu au moins 37 participants nés lors d’une pleine lune pour que notre p-value passe en dessous du seuil de significativité fixé à 0,05(=5%).